人工智能 --- Python求解线性和非线性规划问题
基于jupyter notebook的Python编程
1、线性规划中的单纯形法、大M法的excel求解、python编程求解和python包求解;
2、非线性规划的拉格朗日乘子法的手工数学推导、python编程和python包求解;
一、线性规划问题求解
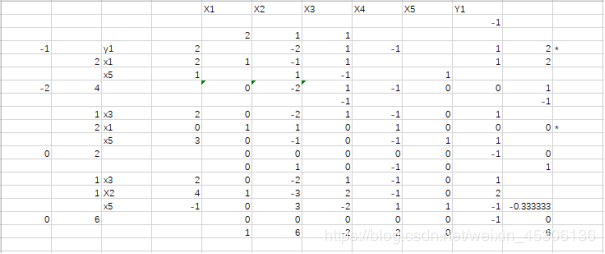
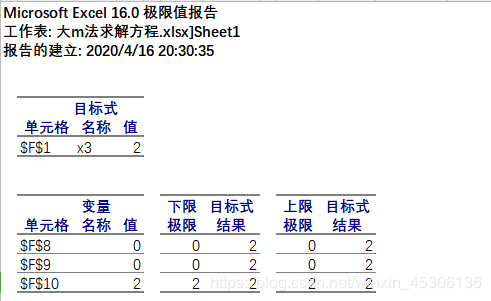
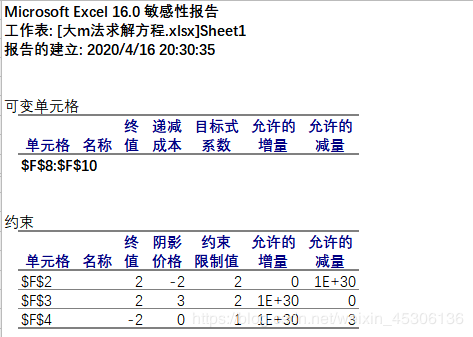
1、Excel中大M法与Excel的“规划求解”包对实际问题的求解比较
实际例题:
求解以下约束条件的线性规划的最大值和最优解
作者:づ如影随行とじ
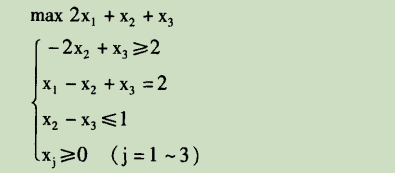
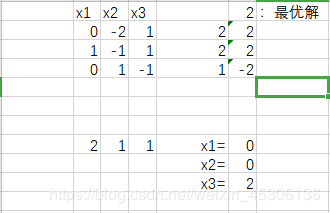

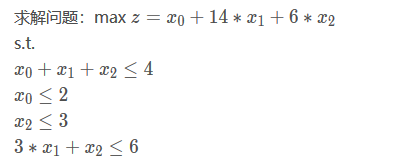

import numpy as np #导入相应的库
import sys
def solve(d,bn):
while max(list(d[0][:-1])) > 0:
l = list(d[0][:-2])
jnum = l.index(max(l)) #转入下标
m=[]
for i in range(bn):
if d[i][jnum] == 0:
m.append(0.)
else:
m.append(d[i][-1]/d[i][jnum])
inum = m.index(min([x for x in m[1:] if x!=0])) #转出下标
s[inum-1] = jnum #更新基变量
d[inum] /= d[inum][jnum]
for i in range(bn):
if i != inum:
d[i] -= d[i][jnum] * d[inum]
def printSol(d,cn):
for i in range(cn - 1):
if i in s:
print("x"+str(i)+"=%.2f" %d[s.index(i)+1][-1])
else:
print("x"+str(i)+"=0.00")
print("objective is %.2f"%(-d[0][-1]))
d = np.loadtxt("F:/data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) #基变量列表
solve(d,bn)
printSol(d,cn)
运行结果:
x0=0.00
x1=1.00
x2=3.00
x3=0.00
x4=2.00
x5=0.00
x6=0.00
objective is 32.00
2.3 Python使用scipy库对实际线性规划问题的求解
整体代码如下:
#导入包
from scipy import optimize
import numpy as np
#确定c,A_ub,B_ub
c = np.array([1,14,6])
A_ub = np.array([[1,1,1],[1,0,0],[0,0,1],[0,3,1]])
B_ub = np.array([4,2,3,6])
#求解
res =optimize.linprog(-c,A_ub,B_ub)
print(res)
运行结果:
con: array([], dtype=float64)
fun: -31.99999999819265
message: 'Optimization terminated successfully.'
nit: 4
slack: array([6.62327970e-11, 2.00000000e+00, 3.88720167e-10, 3.41993101e-10])
status: 0
success: True
x: array([3.06911596e-10, 1.00000000e+00, 3.00000000e+00])
从代码中可以发现
c:c指的应该是要求最大值的函数的系数数组
A_ub:A_ub是应该是不等式未知量的系数矩阵,也就是不等式左边
B_ub:B_ub就是不等式的右边了,也就是不等式右边
3、结果对比分析
3.1 单纯形法结果



![]()
#导入sympy包,用于求导,方程组求解等等
from sympy import *
#设置变量
x1 = symbols("x1")
x2 = symbols("x2")
alpha = symbols("alpha")
#beta = symbols("beta")
#构造拉格朗日等式
L = 60 - 10*x1 - 4*x2 + x1*x1 + x2*x2 - x1*x2 - alpha * (x1 + x2 - 8)
#求导,构造KKT条件
difyL_x1 = diff(L, x1) #对变量x1求导
difyL_x2 = diff(L, x2) #对变量x2求导
difyL_alpha = diff(L, alpha) #对alpha求导
#求解KKT等式
aa = solve([difyL_x1, difyL_x2, difyL_alpha], [x1, x2, alpha])
print(aa)
运行结果:
{x1: 5, x2: 3, alpha: -3}
2.2 python使用SciPy库实现求解问题
python代码如下:
from scipy.optimize import minimize
import numpy as np
#目标函数:
def func(args):
fun = lambda x: 60 - 10*x[0] - 4*x[1] + x[0]**2 + x[1]**2 - x[0]*x[1]
return fun
#约束条件,包括等式约束和不等式约束
def con(args):
cons = ({'type': 'eq', 'fun': lambda x: x[0]+x[1]-8})
return cons
if __name__ == "__main__":
args = ()
args1 = ()
cons = con(args1)
x0 = np.array((2.0, 1.0)) #设置初始值,初始值的设置很重要,很容易收敛到另外的极值点中,建议多试几个值
#求解#
res = minimize(func(args), x0, method='SLSQP', constraints=cons)
print(res.fun)
print(res.success)
print(res.x)
运行结果:
17.000000000000007
True
[4.99999994 3.00000006]
3、Python求解结果对比分析
3.1普通法求解结果
![]()
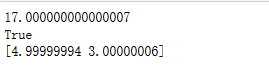
作者:づ如影随行とじ